近日，中国科学院海洋研究所李晓峰研究团队基于深度学习技术，提出了一种高效求解海洋动力学偏微分方程（PDE）的新方法，并成功应用于描述海洋内孤立波的KdV方程组求解。

本研究改进了物理信息神经网络（PINN），引入径向基函数（RBF）代替传统神经网络，提出了PIRBF模型。针对孤立波的强非线性特性，研究团队设计了渐进式学习策略，有效抑制了训练中的误差增长，大幅提升了模型精度和收敛效率，可精准模拟多种形式的孤立波解，包括孤立波解、conidal解和dinodal解，为海洋动力学PDE的高效求解提供了新思路。

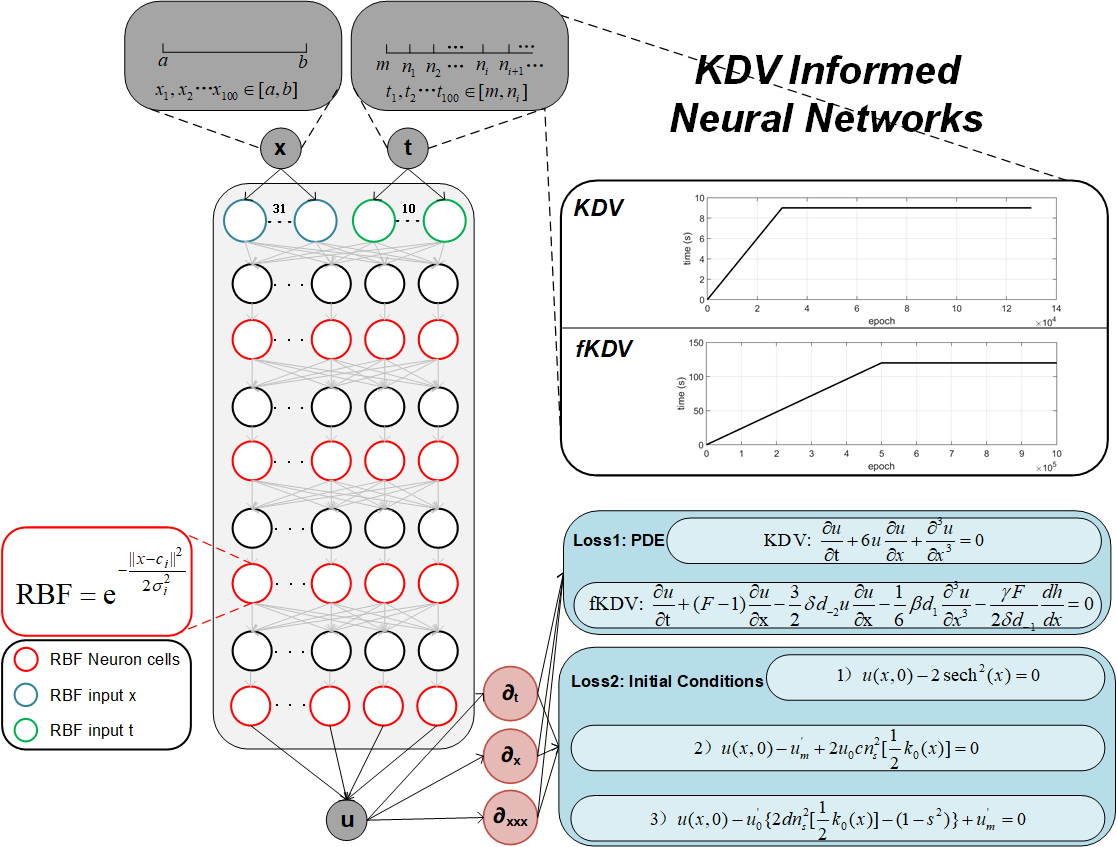
PIRBF模型的结构

该研究的核心亮点在于模型通过自监督学习，仅依赖PDE及初始条件，无需传统数值模型结果作为训练基准，直接利用深度学习技术求解。该方法在求解KdV及其强迫方程（如fKdV方程）时更加灵活，仅需调整偏微分项即可，展现出卓越的精度与效率。同样方法适用于求解薛定谔和Burgers等复杂PDE。模型训练完成后，可在数秒内生成高精度结果，大幅缩短计算时间。研究团队表示，这一技术的成功应用展现了物理驱动深度学习在海洋动力学PDE求解中的广阔前景。

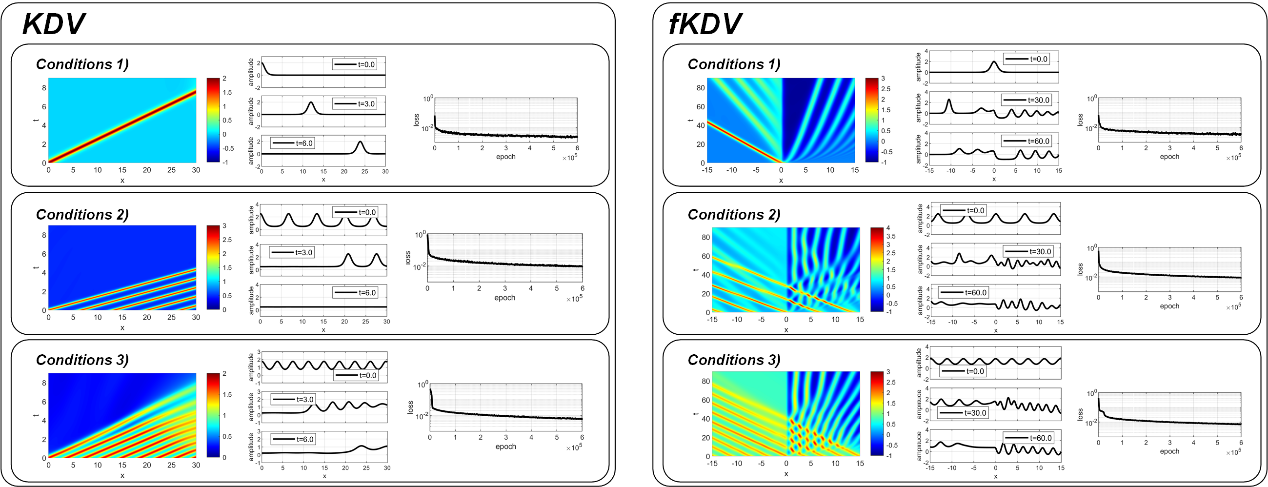
PIRBF模型非线性方程的三个初始条件下 KdV（左）和 fKdV（右）方程的模型结果

本论文第一作者为李晓峰研究员，第二、第三作者为博士研究生王浩宇和杨艺，通信作者为张旭东副研究员。研究工作得到了中国科学院战略重点研究计划及国家自然科学基金项目等资助。

论文信息：

X. Li,H. Wang,Y. Yang,X. Zhang,Deep Learning-Based Solution for the KdV-family Governing Equations of Ocean Internal Waves. Ocean Modelling,102493 (2024).